Utility poles carry high-voltage transmission wires, lower voltage distribution wires, communications lines and transformers. Leaning poles are more liable to crack, bringing the transformer crashing down and hurting people or damaging property in the process. Even lower voltage distribution lines can cause severe injuries. Tree branches that touch a power line can energize the tree and the ground around it, making for a dangerous situation.
It is not all that unusual to see leaning power lines; more often they are distribution poles that carry a lower amount of power to homes and commercial properties. Distribution poles can be subject to formulaic approaches to installation that can ignore soils, weight loads and, most frequently, slopes. Poles are frequently installed on sloping ground or on the sides of ditches because a certain amount of clearance from roads and private property must be maintained. The issue with setting poles on slopes is a loss of lateral soil support on the downhill side of the pole.
Any number of events can compromise pole support and cause several types of concern — water erosion from heavy rain, more weight from newer, heavier components and communications lines mounted on poles, construction damage or ice storms that add weight on wires, and high winds are just a few.
The following photos (Photos 1 and 2) taken from both ends of the pole line show the effects of a snow storm on distribution lines. The ground was wet and not frozen enough to support the poles. Note severely leaning pole B set on a steep slope with no set-back. This is a clear illustration of the problem of setting poles on slopes. It is clear that pole A and pole D are set in a nearly flat area. Their embedment is stable with sufficient strength to prevent leaning. Obviously pole A and D are contributing to the support of pole B and C. If all four of these poles were set on a slope similar to pole B and no supplementary support was provided from adjacent poles, they would likely all fail and fall into the road.
The photos show a progressive failure as the amount of support weakens as the ditch deepens. Like this instance, failures occur in the middle of a section. When the span length doubles, the stress load rises four times, damaging the next poles until the wire lies on the ground, stopping the increase of tension.
Storms will cause more damage to lines going in one direction. East and west running lines will be damaged by one storm while north and south ones will not be. But the next storm, well, wait and hope. This occurred in the March 24, 1978, “Good Friday” storm in 24 Illinois counties. Most of the north and south lines were ruined, knocking power out to about a million people. This is because a storm front usually moves — and does its damage — in one direction.
Other reasons for pole damage
After a storm, practical reasons take over for not reinstalling poles so that they can withstand the next one. Fixing poles can be the last on a utility’s list after all the measures are taken to restore power. It is easier to take the expedient route and dig another hole to reset the pole, but often the hole is not deep enough, sometimes because the standard digger derrick can’t go deeper than 10 feet. The hole can be backfilled with crushed aggregate, but it is a marginal improvement, is cost and labor intensive and may still fail.
Poles that were put up decades ago, particularly in rural areas, are carrying more weight than their original designs anticipated. There are larger and more conductors and more communications and data lines. When new fiber optic lines are added, the old copper cables are often left on poles. For example, a joint user agreement may stipulate that the user must pay for changing poles out for clearance and heavier loads, but that would incent the users to bury their lines underground, and the utility would lose annual pole fees.
An approach to pole setting on sloping ground
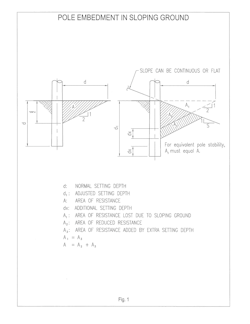
For poles set on continuously sloping ground, or at the top of a road ditch, there is a loss of lateral soil support on the downhill side of the pole. Fig.1 illustrates this loss of support and how it can be replaced. It becomes more complicated if the pole is set back from the top of a slope or the slope ends in a shallow ditch or one with a non-uniform cross section.
If no adjustment is made for this lost support, these poles will lean towards the downslope and in some cases, fall. It is not unusual to see several poles along the top of a road ditch all leaning towards the road. This is especially true on multi-phase lines where poles are heavily loaded, and taller, higher class poles are required but standard setting depths are used.
In some cases, when poles are heavily loaded, and the soil strength has been reduced because of rain or thawing or other reasons, they can fall into the road. If the soil strength of the adjacent poles has not also been reduced, these adjacent poles may take up part of the load and prevent complete collapse (see Photos 1 and 2).
This paper suggests an approach for determining the additional setting depth required to compensate for this loss of support for those situations. The solutions provided are only an approximation of the additional setting depth required. An exact solution is not possible and is not warranted for several reasons.
First, there is often no information on the soil properties other than a visual observation of the surface at the site during staking by personnel untrained in soil properties. Additionally, the ground surface is not always on a neat, constant slope nor is the top or shape of the ditch sharply defined. There are also the uncertainty of the failure surface and the approximation of the estimate of the ground slope.
We include a method to compensate for the effect of a pole being set back from the top of a slope and also a method to compensate for ditches that are shallow or narrow enough to reduce the additional setting depth that would be necessary for a continuous slope.
There has been no attempt to analyze the situation where the force is always in the direction of the upward slope, such as an un-guyed small angle or tap structure. However, if the solutions presented here are used, the results should be more than adequate and somewhat overly conservative. No additional setting depth is required for slopes flatter than a ratio of 2 horizontal to 1 vertical or for ditches shallower than the critical depth. Guyed structures, of course, need no additional setting depth.
Is standard depth appropriate?
Before deciding how much additional setting depth to use, a determination should be made on whether the standard depth is the appropriate depth for flat ground. For a weak pole that is not loaded to its capacity, something less than the standard depth may be adequate. No additional setting depth to compensate for sloping ground may be needed.
For a very strong pole loaded to near capacity, additional depth should be considered even on flat ground. The setting depth of these adjustments is considered the “normal setting depth” used for all subsequent calculations and graphs. If improved backfill is used for normal setting depths, it should also be used for poles requiring extra setting depths.
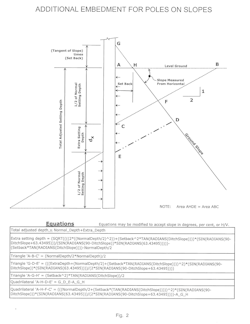
Here is a simplified method of determining if a pole needs to be set deeper. The assumption is that a wedge of soil must be moved laterally and upward for the pole to lean. This wedge is assumed to be the depth of one half the pole’s normal setting depth (approximately at the point of rotation) with a slope of two horizontal to one vertical.
When the soil supporting a pole fails, the pole falls, and as it falls, there is a point below ground line about which the pole essentially rotates. Visualize it as the pole top going one way, and the butt going the other way, pivoting as if a large pin or axle was through the pole about half way between ground line and the butt. The actual rotation point is rarely at this theoretical location but will not vary by much in most soils.
Neither of these assumptions is exact but they simplify the math and provide a reasonable depth of wedge and a reasonable slope for ordinary soils. The point of pole rotation in uniform soils is greater than half the setting depth and the slope of the wedge will vary depending on soil properties. Given these approximations, the results are still reasonable and consistent.
The resistance to movement is assumed to be the friction along both of the triangular sides of the wedge. This is a reasonable approximation of the actual resistance. It ignores any curvature of the failure surface and the friction along the base of the wedge. Additional setting depth would be affected less by these than the side friction, so the result will be on the safe side. A derivation of the equations and an illustration are in Fig. 2.
Depth calculations
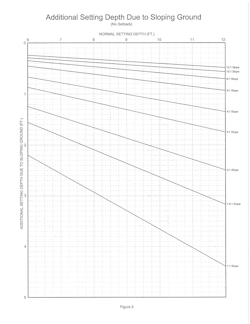
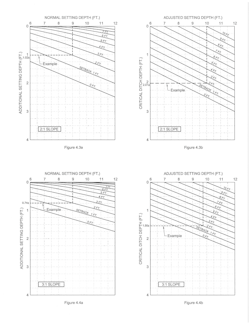
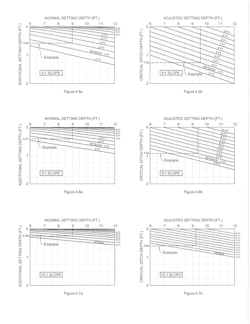
Fig. 3 is a graphical solution for additional setting depth for poles with normal setting depths from 6 to 12 feet on continuous slopes, from 1 horizontal to 1 vertical up to 12 horizontal to 1 vertical and without any setback. The setting depth is always measured on the down-slope side of the pole.
Where poles are set some distance back from the top of a slope, this additional support allows a reduction of the increased setting depth. When the setback equals the normal setting depth, additional setting depth is no longer required.
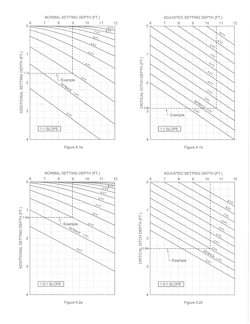
Graphical solutions for poles with setbacks from one foot up to the normal setting depth and normal setting depths from 6 to 12 feet and ground slopes from 1 horizontal to 1 vertical up to 10 horizontal to 1 vertical are shown in Fig. 4.1a through Fig. 4.7a. The number of increments provided should be sufficient to allow reasonable interpolation for intermediate values. The range is probably beyond what most people would consider relevant.
A more efficient method of determining additional setting depth is to program the equations into a hand-held device to accept the variables of setting depth, slope and set-back, and calculate the additional setting depth required.
If a ditch is shallower or narrower than a certain critical depth or width, further reductions in setting depth can be made. This critical depth is shown graphically in Fig. 4.1b through Fig. 4.7b. The critical width Cw is the critical depth Cd multiplied by the slope plus 2 or Cw = Cd(s+2), where s is the horizontal distance for one foot of fall.
A diagram is included showing a typical ditch divided into one fourths vertically and horizontally (see Fig. 5). If the actual ditch is shallower or narrower than the critical ditch, or an irregular cross-section, one can estimate the reduction in each direction and count the number of 1/16ths of the area that are reducing the critical area and adjust the additional setting depth accordingly. Four examples using different fractions of critical depth and width are included.
It would be expected that the fractional ditch dimensions would be determined by visual observation, although measuring instruments could be used. In most real-world situations for distribution lines, this adjustment will be minor and can often be ignored.
Soil considerations
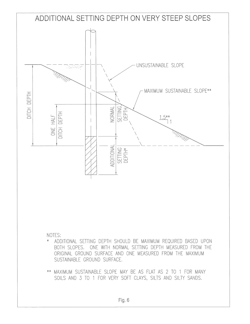
For most ordinary soils, a slope greater than 1.5 to 1 or even 2 to 1 cannot be maintained. For some very soft clays, silt and silty sands this maximum slope can be as low as 3 to 1. If steep slopes in soils of this nature are encountered, it should be assumed that because of erosion, freeze-thaw action, animal activity and gravity, they will deteriorate to the below values (see Fig. 6). The best approach is to avoid this situation. If avoidance is impossible, the pole setting depth should be adjusted as shown in the figure. For very long slopes, this may prove to be impossible.
Field application: Accurately measure slopes
The only new staking requirements, beyond normal line staking activities, are measuring the slope, set-back, ditch depth and sometimes ditch width. After some experience, most of these measurements can usually be done simply and probably with enough accuracy by visual estimation. For unusual conditions, more sophisticated means should be used for all values.
Slope is the most critical element and should be measured with some degree of accuracy beyond visual observation or at least visual observations should be rechecked periodically. Fortunately, most people estimate slopes steeper than they actually are, and the result is greater embedment than is required and on the safe side.
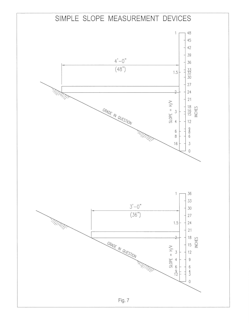
Set-back can be measured by any number of measuring instruments. A simple means to measure slope is to use two laths or even yard sticks. One is held vertical and one horizontal and the respective measurements are recorded and converted to slope, H/V. Or the horizontal lath can be made a constant dimension such as three or four feet and the vertical lath calibrated to read slope directly (see Fig. 7). Many other methods are available.
Ditch depth can be measured using GPS or a hand level and level rod or any other vertical scale. For ditches shallower or narrower than the critical ditch dimensions, a mathematical solution for all the different variations becomes too complex and can’t be justified. It’s suggested that the designer visually estimate the shape and dimensions of the ditch and compare it to Fig. 5 and adjust accordingly.
Conclusion
The information presented should give line designers the information required to determine with consistency the additional depth poles need on sloping ground to compensate for the support lost on the down-slope side of the pole.
Acknowledgement
This paper is inspired by the leadership of the now deceased Marlyn Schepers, who retired on April 10, 1998, after 42 years as a highly respected structural and design engineer at Stanley Consultants. Marlyn championed mundane issues, like pole stability, or lack thereof, mentoring line designers, including the presenter of this paper, with a simple method to incrementally adjust pole setting depth when encountering sloping terrain.
Disclaimer
Presented here is one person's ideas. Others may choose differently. There is no intent here to include sufficient reference materials to do a complete design. Anyone who chooses to use these concepts should first carefully review their own ideas before making the decision to accept, reject or modify.
Stanley Consultants is T&D World media partner.
