Solve This: Wha’ Happened?
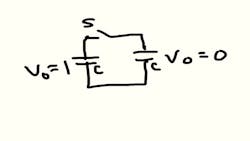
Joe and Moe are roommates at Grindemdown Polytechnic. Joe is a physics major and Moe is a student in electrical engineering. One night they realize that they have the same homework problem: "A capacitor of one Farad is charged to a voltage of one volt. It is connected in parallel through an open switch to an identical capacitor that has zero voltage. The switch is then closed. What is the final voltage across the two capacitors? For simplicity, assume the connections have no resistance and there are no other resistive losses."
Moe sketches the circuit on the dorm room white board:
"That's so easy" says Joe. "I'll just apply my superb understanding of the Law of Conservation of Energy and whip the answer right out!"
"Well,” laughs Moe, “we EE's understand and love electrons. So I'm going to apply the Law of Conservation of Charge."
After a minute or so they compare their answers.
Much to their surprise, the answers don't agree. But neither student made an error in his calculations.
How can that be??
The winner is...Kabdulla!
ANSWER: Both Lynn Schultz and kabdulla are correct about the difference between the two methods of calculating the final voltage. But Kabdulla wins the gift card because of his very thoughtful, detailed discussion.
However, the conclusions about the lost energy aren’t justified. The problem is the discontinuity in the equations. We’re only applying simple circuit equations here – not Maxwell’s E&M theory. If the resistance is really zero then when the switch is thrown then by Ohm’s law the current becomes infinite for an infinitesimal time period – a Dirac delta function if you will. And if you use Ohm’s Law with zero resistance the answer is undefined. Ohm’s law doesn’t consider radiation. Even with any resistance in the circuit, charge is accelerated and therefore by E&M theory energy is radiated. But Ohm’s law doesn’t account for the radiation and, with any resistance in the circuit, no matter how small, we compute that the final energy is the same as the initial - a wrong conclusion though we usually ignore that fact because the error is small unless we’re dealing with wavelengths as small as the physical circuitry, which then acts as an antenna.
Of course we use Ohm’s law all the time with AC and other circuitry where the charges are being accelerated and it gives us adequate accuracy but it never accounts for radiation losses.
Bottom line – with zero resistance we can’t justify any assumptions regarding energy in the final state but we can assume charge is conserved.
Disagree or have a better answer? Comment below. Arguments welcome!
Paul Mauldin